11yu on Tech for Diffusion Image Gens
NOTICE: The guide has moved here and this rentry will no longer get updates.
- Preamble
- Sampling
- Schedulers
- Guidance
- Special Thanks
- Other Guides
- Update History
- References
Preamble
Greetings. You may know me as 11yu from various botmaking / image gen discords.
This rentry is mostly made with SDXL/local in mind, and is not a good introduction to image gen with SD. You can check out some #other guides for that. Instead, I'll be focusing more on:
- 1-2 steps further into the technical aspects of what a usual SD guide may provide.
- This hopefully means somewhere between guides that say "Use X (if Y)" with little to no explanation, and those that dive head first into the meat and potatoes with heavy math equations and terminology hell.
- lesser-known tips, tricks, and technologies that may improve your image gen process.
Everything here should be taken with a mountain of salt, as in practice, other variables could influence your results greatly. Also, this article is mostly written by a dumb person (me). You will likely come out of a section thinking: "Interesting. This doesn't help me at all."
Sections with [TECHNICAL] include a bit more math or complicated subjects. I'll try my best to not use these, but some things are best explained with equations and numbers.
Sampling
Sampling is the technical term for generating an image with a diffusion model. It's called sampling because the idea is we're taking a sample of the original data distribution - that is, we're trying to generate an image that would be similar to real images that we used to train the model.
What is a Sampler?
A sampler is something that decides the way we sample; a method that denoises an image. This process can be modeled as a differential equation (DE) with a given initial condition - which is why "samplers" can be thought of as solvers for DEs. In fact, a good amount of samplers were conceived by starting with this idea.
Getting exact solutions to DEs is usually a very tall order. Instead, what DE solvers do is approximate:
- Start at the initial condition.
- Use math to find out in which direction to go next, such that it'll lead them closer to the true solution.
- Walk a little in that direction.
- Repeat 2-3 until a satisfactory result is reached.
A human analogy: this is like if you were now asked to find where the Eiffel Tower is exactly.
- Right now, you're (hopefully) somewhere on Earth.
- You ask some people how to get to the Eiffel Tower.
- Go in that direction for a bit.
For example, people may tell you that it's in France. Okay, you could fly to France.
Now you're in France, you could ask the locals. "Oh, go that way a bit." So you go where they point for a bit. - Repeat 2-3 until you get to the Eiffel Tower.
For stable diffusion models, this becomes:
- Start with some point in latent space. (determined by your
seed) - Use math to find out in which direction to go next, such that it'll lead them closer to what the image representing the input should be.
- Walk a little in that direction.
- Repeat 2-3 until it gets close enough to the true image.
One can imagine it like this: Given some noisy image, there is a path invisible to your eyes that when followed, will take you to the completely denoised image. Samplers are like devices that can reveal these paths within a short range, but they have varying accuracy, take a long time to activate, and you can only activate them when standing still.
So, to get the denoised image, you stand still and use the device, then take steps trying your best to follow what's shown to you. If you take small steps and use the device to check for directions often, you'll be following these paths more closely, but it'll take a very long time; If you take large steps and seldom use the device, you'll get to the destination in no time, but the 'destination' will probably be a bit far off from the true location.
How much to walk in (3.) is closely related to the step count and the scheduler you choose. More on that in the schedulers section.
Terminology Usage
I'll be using the terms "sampler," "DE solver," "solver," "numerical methods," etc. interchangeably because they basically refer to the same thing.
"Accuracy / Control" = Better?
You've probably seen something along the lines of this in other SD guides:
DPM++is better [thanEuler] for precision and control.
Armed with the perspective that samplers = equation solvers, it's clearer what "precision," "control," and "accuracy," among other similar descriptions really mean - solving the diffusion equation more accurately.
In math terms, we'd say that the solver is "higher order." You can just remember it as "high order = more complex and accurate (in theory)."
However, we are not looking to solve equations, we're looking to generate nice images. Numerical accuracy does not directly equate to good-looking images.
For example, despite the popularity of euler(_ancestral), you may be surprised to find that it's actually the simplest and most inaccurate DE solver. The errors manifest as blurring the output and create a soft/dreamy visual style that many find pleasing.
On the other hand, inaccuracies may also mean small detail is lost - distant buildings merging together, hair strands forming blobs, etc. In severe cases, this might lead to worse prompt adherence overall (the errors are so big that it visibly deviates from your prompt; there's also the factor of the model simply not understanding you, though).
DEs that represent the process of diffusion are often very "stiff," especially at high CFG - this increases numerical instability and in practice:
- makes
adaptivesolvers take many tiny steps, which in turn makes image gen take very long - means that higher order solvers might do worse than expected or completely break, especially with low step count
This may be why the community favorites - euler_ancestral and dpmpp_2m - are "only" first-order and second-order DE solvers respectively but still perform very well.
(And dpm(pp) side-steps the stiffness issue using clever math tailored for diffusion equations.)
Info
Did you know that as originally formulated, a diffusion model has to take 1000 steps to generate an image? What we're doing now all seems like "low step count" compared to that!
[TECHNICAL] How Does Order Affect Error?
Oversimplification
I'll be brushing over many details and oversimplifying things for ease of understanding here. For more accurate information on this topic, see Truncation error.
The "order" of a DE solving method measures how much the errors scale down when you decrease the step size - or equivalently, increase the number of steps.
Let's assume for simplicity, that the error of any sampler taking 1 step is 10. As in, by some measure, the difference between the truth and the answer produced by the solver is 10.
Now, let's take euler, heun, and bosh3, which have an order of 1, 2, 3 respectively, and look at the error at various steps:
| steps | euler |
heun |
bosh3 |
|---|---|---|---|
| 2 | 10 / 2 = 5 |
10 / (2*2) = 2.5 |
10 / (2*2*2) = 1.25 |
| 3 | 10 / 3 ≈ 3 |
10 / (3*3) ≈ 1.1 |
10 / (3*3*3) ≈ 0.37 |
| 4 | 10 / 4 = 2.5 |
10 / (4*4) = 0.625 |
10 / (4*4*4) ≈ 0.156 |
n |
10 / n |
10 / (n*n) |
10 / (n*n*n) |
In general, if the order of a sampler is O, and the error it makes when you take 1 step is E, then the error if you take N steps would be around E / (N^O), where N^O means N multiplied by itself O times, a.k.a exponentiation.
Let's compare euler and heun. heun takes twice as long as euler per step, and has an order of 2. Now, let's run them for the same amount of time and see what happens to the error:
eulerfor 10 steps, then the error is about10 / 10= 1heunfor 5 steps (because it takes 2x as long), then the error is about10 / (5*5)= 0.4
So, in theory, you can get a more accurate result in the same amount of time - or equivalently, get an as accurate result in less time - using higher order samplers, though this only holds true if the extra time needed to achieve higher order isn't too high.
The high stiffness that most diffusion DEs exhibit also makes high-order samplers do really poorly in low steps (or even just in general).
How Fast is My Sampler?
The most computationally expensive thing you can do when diffusing is running the neural network on some inputs. Thus, the iteration speed of a sampler is mostly determined by how many times it needs to run the neural network per step. Running the neural network is also sometimes called "calling the model," doing a "model call," etc.
This is also why you don't see people in research comparing sampling methods in number of steps, but rather Number of Function Evaluations (NFE), which is basically how many times the model was run. It wouldn't make practical sense to compare say euler and heun both at 20 steps, because the latter would have twice the NFE and run for twice as long.
Steps is Not Time Spent
Be on the lookout for potentially misleading statements, such as: "dpmpp_sde is great for low steps sampling." While technically true, dpmpp_sde does 2 model calls per step, which means that in the time dpmpp_sde runs for 5 steps, you could've run say dpmpp_2m for 10 steps.
If you want to make speed-quality comparisons, prefer measuring in NFE over step count. Make sure you don't accidentally compare something like dpmpp_2s_ancestral with dpmpp_2m at the same amount of steps.
Types of Sampling Methods
adaptive
Samplers that choose their own steps, ignoring your setting for step count and scheduler. In some implementations, steps may instead be used as the "max steps" before it's forcefully stopped lest it takes too long.
Stochastic (SDE, ancestral (a), Restart)
Samplers that inject noise back into the image. They never converge - with higher and higher step counts, they don't land on 1 final image and keep refining, instead, the composition may drastically change even if it's very late down the line.
The overall quality of images generated based on non-stochastic vs. stochastic sampling depends on step count:
- low steps: samplers make a few big errors (low steps, high step size). Non-stochastic samplers usually make errors smaller than stochastic samplers if you compare 1 step of each. Thus, non-stochastic methods do better than stochastic methods in low steps.
- high steps: samplers make many small errors (high steps, small step size), which build up over time. It's now the accumulated error affecting image quality the most, and the random noise introduced by stochastic methods can gradually correct them. Thus, stochastic methods do better than non-stochastic methods in high step counts.
Stochastic Methods In Low Steps
Many new stochastic methods try to incorporate the best of both worlds, working nicely even in low steps. This includes Restart, er_sde, and seeds.
VP / VE: Why Some SDE Samplers Break SD3 / Flux
In the original paper that models diffusion as an SDE, they note these ways of doing it:
- Variance Exploding: In the forward process, the variance of the data increases to infinity as time progresses
- Variance Preserving: In the forward process, the variance of the data stays bounded to a reasonable value
- sub-VP: Mostly unimportant for our discussion here
SD3, Flux, AuraFlow, and potentially more to come, all use an architecture based on Rectified Flow (RF), which is very sensitive to the variance. Without careful calibration (a lot of mathing), chances are the noise you add + the step taken is not VP, thus breaking these models. This is why people weren't having luck using anything ancestral or sde etc. on them.
singlestep (s) / multistep (m)
Clarification on Their Naming
"single"step methods are called such because they only use information from the most recent step for calculations, while "multi"step remembers information from multiple previous steps.
| Feature | Singlestep (s) | Multistep (m) |
|---|---|---|
| How it works | Runs the model multiple times each step for better accuracy | Considers multiple previous steps for better accuracy |
| Model Calls per Step | k |
1 |
| Speed (per step) | k times slower than 1 euler |
Basically as fast as euler |
| Accuracy | High | Lower than singlestep |
| Example | dpmpp_2s_ancestral (2 model calls per step = 2x slower than euler) |
dpmpp_2m (same speed as euler) |
Why Do Multistep Methods Have Lower Accuracy?
Though reusing information from older steps makes multistep methods really fast, it's not without its downsides, namely that they might be a bit outdated and not be as applicable to the current step, hence the slightly lower accuracy than singlestep methods.
Implicit / Explicit
2 approaches used to solve DEs.
Effectively, implicit methods take longer but are more resistant to stiffness. This means in theory, you can use higher order implicit methods without them breaking, leading to moar accuracy. (This is super slow, though.)
ALL common samplers are explicit. This includes euler, deis, ipndm(_v), dpm(pp) family, uni_pc, RES, and more.
The quality-speed tradeoff of implicit methods seems to limit their popularity. They're also not found as defaults in popular UIs, so that doesn't help.
Where Can I Find Implicit Samplers?
ComfyUI: RES4LYF
Training-Free / Training-Based
Training-free methods are those that you can use without further changing the model in some way. In other words, you can simply load the model in and use a training-free sampling method on it and it'll (probably) work. These include familiar faces like euler, dpmpp_2m, etc.
Training-based methods require further modification of the model. This would include LCM, Lightning, Hyper, etc. where in order to use them you need to download a separate version of a model or use a LoRA. The upside is generating images in vastly lower steps like 8 or 4.
Though sometimes they come along with a dedicated sampler like lcm, they may work in tandem with training-free samplers in general. For example, you can probably use any of euler, dpmpp_2m, and more on a model with a Hyper LoRA applied.
(Non-exhaustive) List of Training-Free Samplers
At the beginning of each section, you may find a table summarizing the samplers mentioned in the section.
| Sampler | Speed | Order | Converges | Notes |
|---|---|---|---|---|
| Name of the sampler | How many times slower than euler. 1x=the same as euler, 2x=takes twice as long as euler, etc |
The order, as mentioned in #accuracy/control = better?. Some technically support a range of orders, in that case, I'll include the default & range. | Yes (refines 1 image with more steps) / No (may change composition with more steps) | Some notes about the sampler |
Explicit Runge-Kutta Methods: Euler, Heun, and Beyond
| Sampler | Speed | Order | Converges | Notes |
|---|---|---|---|---|
euler |
1x | 1 | Yes | Simplest and most inaccurate, makes soft lines & blurs details. |
euler_ancestral |
1x | 1 | No | Like euler but divergent (adds noise), popular. |
heun |
2x | 2 | Yes | Can be thought of as the "improved" euler |
bosh3 |
3x | 3 | Yes | 3rd order RK |
rk4 |
4x | 4 | Yes | 4th order RK |
dopri6 |
6x | 5 | Yes | 6 model calls/step is needed for order 5. |
euler, heun, and the rarer fehlberg2, bosh3, rk4, dorpi6, and more, all fall under the umbrella of explicit Runge-Kutta(RK) Methods for solving ODEs. They were developed way before any diffusion model, or even any modern computer, came to be.
RK methods are singlestep, which means that they take quite long to run. bosh3 for example takes 3 times longer than euler per step. Combined with the fact that diffusion DEs are stiff, this means that it's seldom worth using a high-order explicit RK method by itself, as it massively increases sampling time while netting you a very marginal gain in quality.
Personally, I'd at most use bosh3, though even that's cutting it close. It's no wonder that you don't find some of these in popular UIs.
Samplers developed down the road employ optimizations specific to diffusion equations, making them the better choice 90% of the time.
Where Can I Find These Other Samplers?
- ComfyUI: ComfyUI-RK-Sampler or RES4LYF
- reForge: Settings->Sampler according to this
Early Days of Diffusion: DDPM, DDIM, PLMS(PNDM)
| Sampler | Speed | Order | Converges | Notes |
|---|---|---|---|---|
ddpm |
1x | 1 | No | The original diffusion sampler |
ddim |
1x | 1 | Yes | Converges faster than DDPM, trading a bit of quality |
plms=pndm |
1x | default 4 (up to 4) | Yes | LMS tailored for use in diffusion (uses Adams–Bashforth under the hood) |
DDPM was what started it all, applying diffusion models to image generation, achieving really high quality but requiring a thousand steps to generate a sample.
Through adjustments to the diffusion equation, people arrived at DDIM, drastically reducing the number of steps required at the cost of a little quality.
PNDM finds that classical methods don't work well with diffusion equations. So they design a new way to do it - pseudo numerical methods. They then tried many approaches and found that Pseudo Linear Multistep Method (PLMS) seemed the best, hence the other name.
These 3, along with the classical ODE solvers euler, heun, and LMS, were the original samplers shipped with the release of the original stable diffusion.
How are "Pseudo" Numerical Methods Different?
Recall the 2nd and 3rd steps of DE solving in #what is a sampler:
- Find the direction to walk
- Walk in that direction for a bit
Essentially, classical methods walk in a straight line in step 3, however the training data for diffusion models - the safe roads to walk on, if you will - form a curvy path. This means that classical methods may accidentally step outside the safe roads into the danger zones (range of data unseen in training), leading to a bad sample.
So... why not walk in non-straight lines? That's exactly what the authors of PNDM do, and they call these pseudo numerical methods.
Steady Improvements: DEIS + iPNDM, DPM
| Sampler | Speed | Order | Converges | Notes |
|---|---|---|---|---|
deis |
1x | default 3 (up to 4) | Yes | |
ipndm |
1x | 4 | Yes | ipndm found empirically better than ipndm_v |
ipndm_v |
1x | 4 | Yes | |
dpm_2 |
2x | 2 | Yes | |
dpm_2_ancestral |
2x | 2 | No | |
dpm_adaptive |
3x | default 3 (2 or 3) | Yes | ignores steps & scheduler settings, runs until it stops itself |
dpm_fast |
1x (averaged) | between 1~3 | Yes | Uses DPM-Solver 3,2,1 such that the number of model calls = number of steps, effectively taking the same time as euler would in the same number of steps |
DEIS and DPM independently came to the same conclusion: Diffusion equations are too stiff for classical high-order solvers to do well. They use a variety of techniques to remedy this.
Notably, they both solve a part of the equation exactly, removing any error associated with it while leaving the rest less stiff. This idea is so good in fact that many samplers down the road also do it.
The DEIS paper also introduced "improved PNDM" (iPNDM). ipndm_v is the variable step version that should work better for diffusion, though they find empirically that ipndm performs better than ipndm_v.
Differing Results With ipndm_v
In my personal tests in ComfyUI, for some reason, I find for the same exact parameters - prompt, seed, etc. - ipndm_v sometimes breaks (lots of artifacts) if you use KSampler, but not if you use SamplerCustomAdvanced. In fact, I've never gotten any image breakdown with SamplerCustomAdvanced + ipndm_v, unless at low steps where it hasn't converged. Bextoper has also noted that ipndm_v breaks similarly to KSampler in Forge.
Cascade of New Ideas: DPM++, UniPC, Restart, RES, Gradient Estimation, ER SDE, SEEDS
| Sampler | Speed | Order | Converges | Notes |
|---|---|---|---|---|
dpmpp_2s_ancestral |
2x | 2 | No | "dpmpp" as in "DPM Plus Plus" = "DPM++" |
dpmpp_sde |
2x | 2 | No | I think this is "SDE-DPM-Solver++(2S)" not found explicitly defined in the paper |
dpmpp_2m |
1x | 2 | Yes | |
dpmpp_3m_sde |
1x | 3 | No | |
uni_pc |
1x | 3 | Yes | Official repo |
uni_pc_bh2 |
1x | 3 | Yes | Empirically found a little better than uni_pc in guided sampling |
Restart |
default 2x (varies) | default 2 (varies) | No | Speed & order depends on the underlying solver used (paper uses heun); Official repo |
res_multistep |
1x | 2 | Yes | The authors give a general way to define res_singlestep for any order |
gradient_estimation |
1x | 2 (?) | Yes | Uses 2 substeps, so I guess order 2? Not sure if the notion of order really applies... |
seeds_2/3 |
2/3x | 2/3 | No | |
er_sde |
1x | default 3 (1-3) | No | Official repo |
*(this nothing to do with StableCascade I just thought it's a cool title)
Around this time, the idea of guidance took off, offering the ability to specify what image we want to generate, but also bringing new challenges to the table:
- High guidance makes the DE even stiffer, breaking high-order samplers
- High guidance knocks samples out of the training data range (train-test mismatch), creating unnatural images
To address issues with high CFG, DPM++ adds 2 techniques (that were proposed in prior works by others already) to DPM:
- Switch from noise prediction (ε-pred = eps-pred) to data prediction (x₀-pred) (which they show is better by a constant in Appendix B).
- The above also allows them to apply thresholding to push the sample back into training data range.
Practical; Not a Technical Marvel
The dpmpp family, especially dpmpp_2m, are one of the most widely used samplers alongside euler_ancestral. However, it was rejected by ICLR due to heavily relying on existing works, so it "does not contain enough technical novelty."
UniPC came soon after. Inspired by the predictor-corrector ODE methods, they develop UniC, a corrector that can be directly plugged after any existing sampler to increase its accuracy. As a byproduct, they derive UniP from the same equation as UniC, which is a predictor that can go up to any arbitrary order. The two combine to UniPC, achieving SOTA results using order=3.
Restart doesn't actually introduce a new sampler, instead focusing on the discrepancy between trying to solve diffusion as an ODE (no noise injections) vs. an SDE (injects noise at every step). To get the best of both worlds, Restart proposes that rather than injecting noise at every step, let's do it in infrequent intervals.
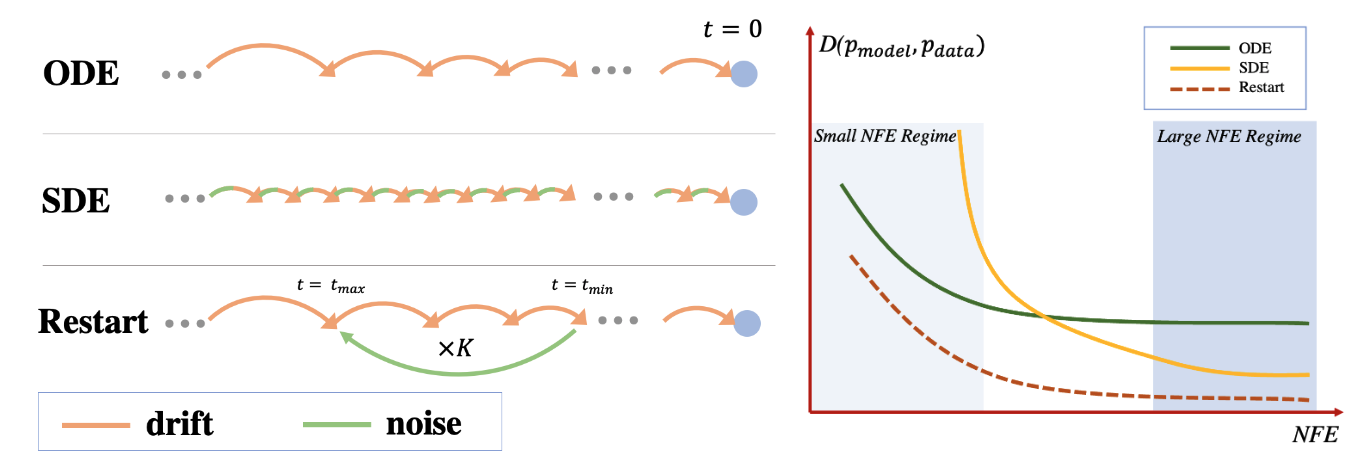
Visualization of ODE, SDE, and Restart taken from their official repo
RES identified an overlooked set of conditions that solvers must satisfy to achieve their claimed order (they find that dpmpp doesn't satisfy some of these, leading to worse-than-expected results). They then unify the equation for noise prediction and data prediction, making analysis easier. Finally, they pick coefficients that satisfy these additional conditions.
Gradient Estimation finds that denoising can be interpreted as a form of gradient descent, and designs a sampler based on it.
SEEDS rewrites a whole lot of equations so that more parts can be solved exactly or approximated more accurately. To make sure the equation stays true, a modified way of injecting noise is used. They derive SEEDS for both eps-pred and data-pred, though the former is very slow so ComfyUI includes only the latter.
ER SDE models the diffusion process as an Extended Reverse-Time SDE and develops a solver based on that.
Out of Reach: AMED, DC-Solver, among Others
With so many samplers, it's no surprise that some have been left out of the party.
This section includes sampling techniques that, while exist in literature or python code, are unavailable in popular UIs that are more accessible to non-coders.
Since they're not widely available, discussion is also low so there will be many more that I simply don't know about and are missing from the list.
Techniques Not Included: (in no particular order)
- UniC: As said before, you could in theory plug UniC after any sampler to achieve better accuracy. No UI lets you actually do that though to my knowledge.
Samplers Not Included: (in no particular order)
(Non-exhaustive) List of Training-Based Sampling Methods
UNDER CONSTRUCTION
This section is incomplete and subject to massive changes.
lcm: Consistency Models defines a new training objective for the model - to learn the "consistency function (CF)," which is some functionf(x, t) = x_0that takes the current noisy image and the time step, and outputs the origin - that is, the completely denoised image. LCM applies the idea to latent-based models (like stable diffusion).- Sampling in 1 step in practice doesn't yield great images. To fix this, they enable it to run multiple steps by re-injecting noise. The procedure is: 1st prediction, inject noise back, predict again, ... repeat.
turbo: Paper authors use both adversarial loss and distillation loss to further train a model to allow it to generate images in a few steps.- Adversarial loss: A neural network (the "discriminator") is used to "detect" if the few-step-generated image is AI-generated; If the discriminator successfully detects it, the image gen model is punished and forced to do better.
The discriminator is also trained by us and not perfect. Only using adversarial loss eventually leads to the model to exploit the discriminator's defects that, while minimizing adversarial loss, results in horrible images. - Distillation loss: During training, which requires the model being trained (the "student") to predict the noise, a different image gen model (the "teacher") also predicts the noise along with it. The student is rewarded if what it predicts is close to what the teacher predicts.
This helps ground the student model to generate sane images and not abuse the discriminator's imperfections.
- Adversarial loss: A neural network (the "discriminator") is used to "detect" if the few-step-generated image is AI-generated; If the discriminator successfully detects it, the image gen model is punished and forced to do better.
lightning: Basically improves upon the methods ofturbo.turboused a pre-trained encoder as the foundation for the discriminator, which introduced several problems like increased training hardware reqs, stuff like LoRAs being less compatible, etc.lightningdirectly uses the diffusion model's encoder as the discriminator's backbone instead.tcd: Authors identify issues on whylcmcan't make clear images with good detail, which is the accumulated errors due to practical limitations during training and sampling. To fix this they:- Update the training objective: They expand the definition of the original CF and arrive at the "trajectory consistency function (TCF),"
f(x, t, s) = x_s. Compared to the original CF, TCF additionally takes an inputs, and outputs the partially denoised image at timesteps(ifs = 0then the output is the completely denoised image again). - Update the sampling method: The new objective being TCD allows them to use stochastic sampling, which helps to correct accumulated errors.
- Several key ideas of TCD are highly similar to that of CTM and the two have a dispute. TCD has been accused of plagiarism by CTM's authors, with there being a response on the same post and TCD's code repo, with CTM's authors being dissatisfied with said response in this issue. I can't find anything that happened afterward.
- Update the training objective: They expand the definition of the original CF and arrive at the "trajectory consistency function (TCF),"
hyper: Takes ideas from CTM and DMD, and incorporates human feedback to train a low-step genning model and LoRA.dmd2: DMD says rather than rewarding the student model for following the teacher model step by step, only reward the final result and ignore how the student does it. This did great but came with problems like high hardware reqs and the student following the teacher step by step anyway, that DMD2 fixes:- Use the Two-Time Scale Rule inspired by this paper, reducing hardware reqs as DMD2 no longer requires generating an entire dataset using the teacher to stabilize training.
- Additionally use a discriminator as well, which potentially allows the student to surpass the teacher.
- 1 step generation still isn't great, so they extend it to support many-step generation like how
lcmdoes it (predict, noise inject, repeat).
pcm: Again inspired by consistency models, rather than predicting the completely denoised image, cut it into multiple intermediate steps and try predicting from one to the next. This also solves the train-test mismatch of what the model was trained for not matching how it's used in practice.
Practical TL;DR of Samplers
Iteration Speed (How Long 1 Step Takes)
| Relative Speed | Samplers |
|---|---|
| 1x | euler, dpmpp_2m (and everything with <number>m in the name), most others |
| 2x | heun, dpm_2, dpmpp_sde, seeds_2, dpmpp_2s_ancestral (and everything with 2s in the name) |
| 3x | heunpp, seeds_3, dpm_adaptive, anything with 3s in the name |
Samplers That Change Composition As You Increase Step Count
ddpmrestartseeds- Any sampler with
ancestral (a)in the name - Any sampler with
sdein the name
Generally, these samplers beat their non-composition-changing counterparts if you use a lot of steps.
What Works at Various Step Counts
| Steps | Works Well | Usually Breaks |
|---|---|---|
| 1-5 | Training-based methods like lcm, lightning, hyper |
Everything else |
| 6-15 | Many (realistically, 6-10 steps will also leave very visible artifacts, but may occasionally be ok.) | ipndm(_v), dpmpp_3m_sde, seeds_3 |
| 16-30 | Mostly everything | dpmpp_3m_sde may still leave artifacts |
| 30+ | High-order methods like ipndm(_v) / Stochastic methods like dpmpp_3m_sde |
- |
"But X Worked/Broke For Me!"
These were tested on an eps-pred model on a few samples. You should see these only as general rules of thumb on what works in low / high step environments.
Schedulers
UNDER CONSTRUCTION
This section is incomplete and subject to massive changes.
What's The Difference Between Samplers and Schedulers?
The sampler controls the way to remove that amount of noise.
The scheduler controls how much noise to remove at each step.
A scheduler is (a way to generate) a list of numbers that quantify the amount of noise in an image (usually denoted using sigma σ).
For generating images, σ starts at a high value (very noisy image) and ends at a very low value (clear images).
The actual values of the highest and lowest σ (σ_max, σ_min) are different across models, which in turn affect the values that schedulers generate, but this isn't something you have to worry about as it's handled by your frontend (A1111, ComfyUI, forge, etc).
For practical training reasons, σ_min actually may not be 0 (which would represent a clean, no-noise image). A 0 is often added to the end of the list to represent that there should be no noise in the final result.
(Non-exhaustive) List of Schedulers
normal: Time uniform sampling that includes bothσ_maxandσ_min- In practice, this may lead to having a final tiny step (
σ_minto 0) that doesn't behave well
- In practice, this may lead to having a final tiny step (
karras: The schedule introduced in EDM by Karras et al.exponential: A schedule where theσfollows an exponential curvesgm_uniform:normal, except thatσ_minis not included- You can probably replace
normalwith this one in all situations - AFAICT, the naming comes from StabilityAI's generative-models repository.
- You can probably replace
simple: comfy wrote the simplest scheduler they could think of for fun. In practice, basically the same assgm_uniform.ddim_uniform: The schedule used in the original DDIM paperbeta: Paper authors found the model settles general composition in the early steps while ironing out small details in the later steps, with "nothing" really happening in the middle steps. They thus argue to use the beta distribution for generating a schedule, which would give more steps to both ends and leave a few steps in the middle.kl_optimal: Introduced in AYS paper that theoretically would minimize the kl divergence.AYS(Align Your Steps): Predefined lists of noise levels found through numerical optimization to be good for a specific model architecture.SD1/SDXL/SVD: Match this with the one your model is based on.AYS 11/AYS 32:AYStuned for 10 / 31 steps generation. If you select any step count besides 10 / 31, log-linear interpolation is used to create the undefined noise levels.
GITS(Geometry-Inspired Time Scheduling): Paper authors examine different image gen neural nets and found surprisingly similar generation trajectories across them. They exploit the structure of this trajectory, which is GITS.
Guidance
UNDER CONSTRUCTION
This section is incomplete and subject to massive changes.
As originally conceived, there was no way to specify the sample generated by a diffusion model. For example, if your training images contained elves and bunnies, you can be sure that your model will generate either an elf or a bunny, but you can't specify which it should generate. If you wanted an elf specifically, your only hope was to run it on many different seeds and pray that one of those seeds made an elf.
This is where "Guidance" comes in. Guidance is the umbrella term for any method that steers the output of the model during generation. This can be anything from text to other input images, OpenPose, etc.
CFG
CFG in Flux
Flux was not trained with CFG, thus nothing in this section applies. The "Guidance" value you can provide to flux is not CFG.
We can see how CFG works exactly by digging through code:
Where uncond_pred is the model prediction without conditioning, and cond_pred is the model prediction with conditioning. cond_scale is CFG, and cfg_result is the result image we get. For brevity, I'll be referring to uncond_pred and cond_pred as uncond and cond respectively. You can imagine that:
uncondis what the model thinks it should do.condis what the model thinks it should do, given our guidance.
Let's play with some CFG numbers:
| cfg | cfg_result |
effect |
|---|---|---|
| 0.1 | uncond*0.9 + cond*0.1 |
The effect that our guidance has is pretty weak. 90% of the generation process is still decided by uncond. |
| 0.5 | uncond*0.5 + cond*0.5 |
The strength of our guidance is on even footing with the unguided conditioning. |
| 1 | cond |
The uncond cancels out, leaving us with only cond. The generation process is entirely decided by our guidance. |
| 2 | 2*cond - uncond |
The model actively moves away from uncond, while the effect that our guidance has increases even more. |
When implementing CFG in practice, people also noticed what we found here - namely that when cfg > 1, the model moves away from uncond. Then, couldn't we use uncond as some sort of opposite guidance - "Do anything but this?" Yes! This is what became negative prompts.
Now with that in mind, let's rewrite the equation in more familiar terms:
Where you can imagine positive and negative as the representation of the positive and negative prompts respectively that the model understands.
Armed with this knowledge, let's reiterate what happens with prompts at various CFG levels:
cfg < 1: Negative prompts would behave like positive prompts.cfg = 1: Negative prompts have no effect.cfg > 1: The model will actively avoid generating anything in the negative prompt.
I also want to note something special about cfg = 1 - that is, the negative prompt having no effect. Couldn't we skip calculating negative entirely then? Yep. ComfyUI does this, which is why you'll see 2x iteration speed if you set cfg = 1.
CFG++
Rescales CFG to work in the range of 0 to 1 making it work better at low guidance scales. It also makes the diffusing process smoother, and may lead to reduced artifacts.
One usually accesses these by choosing predefined samplers, i.e. in ComfyUI euler_ancestral_cfg_pp is euler_ancestral using CFG++.
In my and Bex's personal tests:
- CFG++ samplers give eps-pred models a very good color range, rivaling that of what v-pred models claim to achieve.
- Using CFG++ to inpaint at high steps breaks the image for reasons unknown.
Note that in ComfyUI, the _cfg_pp samplers in KSampler are alt implementations where you instead simply want to divide the CFG you're used to by 2. For example, if you usually run euler_ancestral at CFG=7, you'd run euler_ancestral_cfg_pp at CFG=3.5.
In practice, the reasonable range I find for these is CFG between [0.7, 3], and 1.6 is a sane default to start with.
Special Thanks
My sincerest thank you, to all the people of this community. I would've never thought to make anything like this without yall.
Other Guides
- Bex's Stable Diffusion Tips and Tricks; and General Usage Guide for Illustrious Models
- Skelly's Necronomicon: Art Generating
- StatuoTW's Guide to Making Bots - #Generating AI Art, a Guide to your First AI Gens.
Update History
Changelog:
- 2025 May 2:
- Table-fied many more sections - thanks to @Skelly again
- Grammar fixes - thanks to @kirhn
- Renamed some sections and terms (divergent -> stochastic to be more consistent with literature)
- Added a section on training-based sampling methods
- 2025 April 29:
- Added the Guidance section and the CFG subsection
- Expanded upon the Scheduler list
- Added a note about
ipndm_vsometimes breaking for reasons unknown - Removed "Opinionated Sampler Usage Guide" as I don't think it fits the theme of this rentry
- 2025 April 25:
- Consistency fixes
- Section on VP vs. VE SDE
- Adding to the scheduling section
- 2025 April 23: Consistency fixes & misinfo correction
- 2025 April 22:
- Added "Practical TL;DR of Samplers"
- Table-fied many sections
- Thank you to @Skelly for the suggestion.
- Initial Release
- Samplers section ready
- Schedulers section started
Planned:
- Models
- Samplers: Initial version done
- Schedulers: Under heavy construction
- Guidance
- Rewrite sections if necessary to connect the concepts / make it flow better
References
Other materials referenced in the making of this rentry, that weren't already embedded into their respective sections.
In no particular order:
- sander.ai
- huggingface's
diffusers - A Comprehensive Review on Noise Control of Diffusion Model
- Efficient Diffusion Models: A Comprehensive Survey from Principles to Practices
- Diffusion Models: A Comprehensive Survey of Methods and Applications
- Efficient Diffusion Models: A Survey
- Complete guide to samplers in Stable Diffusion